Euler path is a path in graph that visits every edge exactly once.

• A connected undirected graph has an Euler path but NOT AN EULER CIRCUIT iff exactly two vertices has odd degree.
• A connected directed graph has an Euler path iff each vertex except 2 have the same in-degree as out-degree, and one of those 2 vertices has out-degree with one greater than in-degree (this is the start vertex), and the other vertex has in-degree with one greater than out-degree (this is the end vertex).

Euler circuit is an Euler path which starts and ends on the same vertex.

• A connected undirected graph has an Euler cycle iff every vertex has even degree.
• A connected directed graph has an Euler cycle iff every vertex has the same in and out degrees.

Find an Euler path/circuit

Fleury's Algorithm

O(E * E) - Finds both Euler path and Euler cycle. https://www.geeksforgeeks.org/fleurys-algorithm-for-printing-eulerian-path/

1. Make sure the graph has either 0 or 2 odd vertices.
2. If there are 0 odd vertices, start anywhere. If there are 2 odd vertices, start at one of them.
3. Follow edges one at a time. If you have a choice between a bridge and a non-bridge, always choose the non-bridge.
   1. Bridge: an edge that makes the graph disconnected upon removal.

Hierholzer's Algorithm

O(E) - linear time! But applies to Euler cycle ONLY.

Key points:

• Backtrack, process after finding an dead end.
• Either delete the edge or record it in a map/set during backtrack.
• Reverse the sequence of vertex/edges in the end, or append to the head during backtracking.

332. Reconstruct Itinerary

Simple DFS by building the path backwards upon backtracking.

In the graph below, assume A is the starting point and E is visited before B. When DFS is blocked at F, we return to A and visits B. Since the list is constructed backwards, we still have a valid Eulerian cycle in the end.

class Solution {
    public List<String> findItinerary(String[][] tickets) {
        Map<String, PriorityQueue<String>> map = new HashMap<>();
        for (String[] ticket : tickets) {
            map.computeIfAbsent(ticket[0], x -> new PriorityQueue<>()).add(ticket[1]);
        }

        LinkedList<String> result = new LinkedList<>();
        dfs("JFK", map, result);

        return result;
    }

    private void dfs(String from, Map<String, PriorityQueue<String>> map, LinkedList<String> result) {
        if (map.containsKey(from)) {
            while (!map.get(from).isEmpty()) {
                dfs(map.get(from).poll(), map, result);
            }
        }

        result.addFirst(from);
    }
}

753. Cracking the Safe

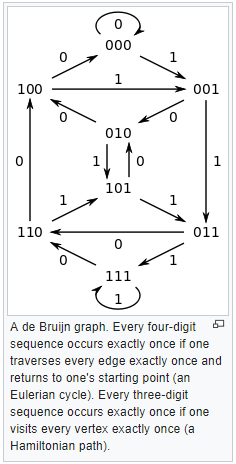
There exist an Euler cycle since all nodes have the same in and out degrees.

class Solution {
    public String crackSafe(int n, int k) {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < n - 1; i++) {
            sb.append("0");
        }

        StringBuilder result = new StringBuilder();
        Set<String> visited = new HashSet<>();

        dfs(k, sb.toString(), result, visited);

        return result.append(sb).toString();
    }

    private void dfs(int k, String node, StringBuilder result, Set<String> visited) {
        for (int i = 0; i < k; i++) {
            String next = node + i;
            if (visited.contains(next)) continue;
            visited.add(next);
            dfs(k, next.substring(1), result, visited);
            result.append(i);
        }
    }
}

Note: does not need to reverse at the end - symmetry